集合是由一组无序的且唯一的项组成的。集合这个结构,可以使用数学概念中的有限集合的概念来类比。在JavaScript中,ECMAScript 6使用Set类对集合进行了实现。
在字典中,存储的是[键,值]对,其中键名用来查询特定的元素。可是使用实际的字典作为类比(单词和它们的释义)。在JavaScript中,ECMAScript 6使用Map类对集合进行了实现。
散列表(hash table)是实现字典操作的一种有效的数据结构。目的呢,就是为了更方便地查询一个元素。下面会是具体介绍。
集合
数学概念中的集合
首先我们来理解数学概念中的集合概念。集合是什么呢,集合就是一堆东西1。
1这是来源于朴素集合论的说法
但是这一堆东西的集合有自己的特性:
- 无序性
- 互异性
- 确定性,给定任一个元素,要么属于这个集合,要么不属于
当元素a属于集合A,则记作a∈A。
Set对象
在JavaScript中,集合使用内建对象Set来表现。这里我们主要是关注它,语法如下:
new Set([iterable]);
所以元素必须是可遍历的基本数据类型或者引用类型。我们举个例子:
var a = new Set();
a.add(1);
a.add("hello");
a.add(false);
console.log(a);
我们来看一下Google控制台的输出:
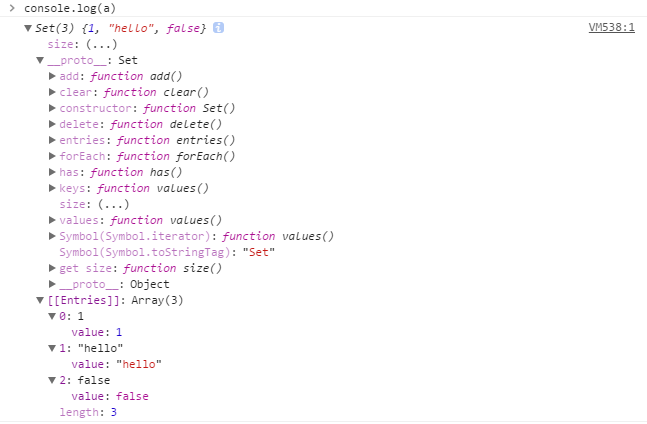
可以看到,这个对象的主要方法有add()、clear()、delete()、has()、values()以及遍历forEach()。如果我们试图使用下标去访问其中的某个元素:
console.log(a[1]);
//undefined
好的,集合就介绍到这。
字典
Map对象
同样的道理,我们看一下JavaScript中的Map对象。语法构造如下:
new Map([iterable])
[key,value]都可以是可遍历的基本数据类型和引用对象。比如,我们用Map来构建一个邮件通讯录。
var dic = new Map();
dic.set('timi','maoxiaoke@outlook.com');
dic.set('maoxioake','thebigyellowbee@qq.com');
dic.set('yuer','yuer@xiaoke.com');
控制台输出:
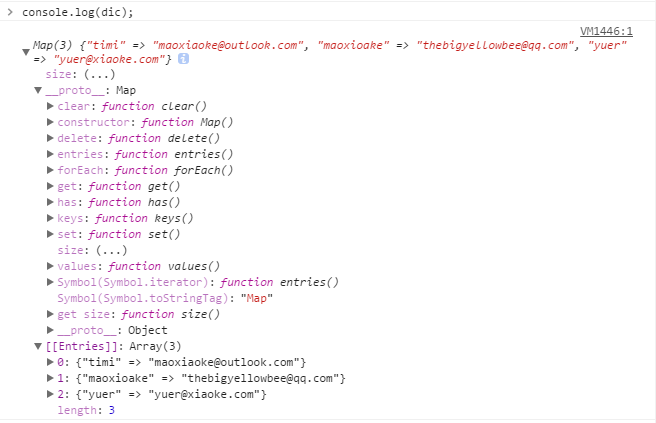
Map对象的方法有clear()、set()、has()、delete()、forEach()。重点我们看一下get()方法。我们用这个方法在字典中获取一个值。
console.log(dic.get('timi'));
// maoixoake@outlook.com
console.log(dic['timi']);
//undefined
大家可以看到和对象的区别了吗?
是的,这不是我们的重点,重点是我们的哈希表。
散列表
正如开头说的,散列表实际就是字典的另一种实现方式,目的就是更快地找到一个值。在常规的字典操作中,使用get()方法获得一个值,需要遍历整个数据结构。为了能在O(1)时间内查找到某个值,我们使用了一种叫做散列函数的方法,通过散列函数,就知道值的具体位置。是如何实现的呢?
首先,多数散列函数都假定关键字的全域(U)为自然数集N = {0,1,2, ...}。因此,如果所给的关键字(指的是key值)不是自然数,就需要一种方法将它们转换成自然数 – 比如,我们使用字母的ASCII值。
这里,我们所给的所有关键字的自然数的集合(
K)是全域的子集。
| 键 | 散列函数 | 散列值 | 散列表 |
|---|---|---|---|
| timi | lose lose | 116+105+109+105=435 | [435] maoxiaoke@outlook.com |
| maoxiaoke | lose lose | 958 | [453] thebigyellowbee@qq.com |
| yuer | lose lose | 121+117+101+114=453 | [958] yuer@xiaoke.com |
在散列值对应的[435]、[453]、[958]位置上,有对应的值。在其他的散列值位置上,是空值。所以说,散列表是普通数组的推广,这样你就可以像使用数组下标一样(这种说法可能有纰漏)使用字典了。
“lose lose”是一种非常简单的散列函数,只是简单地将每个键值中的每个字母的ASCII值相加。这种散列函数的缺点是造成的冲突会比较多。另外,上面表格实际上用的markdown作图,所以在表述上还有不太合理的地方。
所以,使用散列函数来查找一个元素的步骤是: 我们添加一个元素,对应的散列值就会作为识别码替代元素的key值。当我们给出一个元素的key值,我们使用散列函数将其转换成散列值,从而找到对应元素的value值。平均时间就是O(1)。
当然,这不是唯一的一个原因。
如果我们不使用散列表的话,全域U很大,电脑的内存空间恐怕很难支持。而实际的K域可能相对U域很小,这样的话就造成了很大的浪费。所以,我们使用散列函数,实际上就是一种映射。散列函数将大小为|U|的散列表映射成大小为m(m>=0)的散列表。m的最大值由散列函数和key值决定,而且一般比|U|小的多。
所以,这里还会造成一个问题: 就是多个key值映射到同一个散列值上。比如,我们添加两个元素。
dic.set('qznl','qznl@xiaoke.com');
dic.set('CheNg','CheNg@xiaoke.com');
那么,key值为yuer、qznl、CheNg三个元素的散列值都是一样的,为453。好尴尬呀,怎么解决呢。一种为链接法(chaining),另一种称为开放寻址法(open addressing)。
链接法 – chaining
链接法的思想是,把散列到同一个散列值的所有元素都放在一个链表里。如下图:
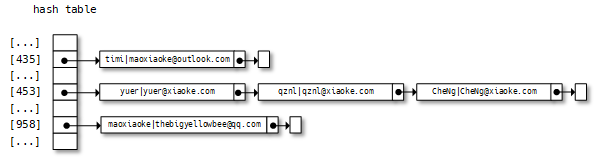
这种方法的缺陷很明显,会增加额外的内存空间。
开放寻址法 – open addressing
虽然说我们的内存空间通过散列函数限制为m大小了,但是散列值并非是等概率分布的。有些散列值可能对应多个元素,有些则包含空。但是,散列表也可能被填满,从而不能插入任何新的元素。所以,这都不是一定的。开放寻址法的思想就是,我们将散列值相同的元素插入那些对应为空的散列值中。
也有多种思路。
线性探查 – linear probing
第一种就是线性探查。当向表中某个位置插入一个新元素时,如果该散列值对应的位置已经被占据了,则尝试散列值+1的位置。如果散列值+2的位置也被占据,则尝试散列值+3的位置,以此类推。
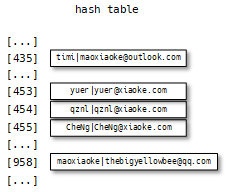
让我们来模拟一下查找操作。当我们想查找一个散列值为453的元素,如果是yuer,查找结束;不是,+1查找找到qznl,如果是,查找结束;不是,+2查找,找到CheNg,如果是,查找结束;不是,+3查找,这里对应为空,元素没有找到,即散列表中没有该元素。
这种方法比较容易实现,但存在一个问题: 一次集群(primary clustering)现象。这让我想到了错误集群现象,就是有bug的地方通常不止一个。
二次探查 – quadratic probing
二次探查就是在后续的探查位置上添加一个偏移量,该偏移量以二次的方式依赖于探查序号i。这种方式比线性探查好的多,但是也会出现二次集群现象。
双重散列 – double hashing
双重散列是用于开放寻址法最好的方法之一。具体就是后续探查的位置是前一个位置加上偏移量对m的取模。
散列函数
上面我们介绍了一种哈希函数lose lose,这不是一个表现良好的散列函数,因为它会产生大量的冲突。另一个比较好的散列函数是djb2。
var djbHashCode = function (key) {
var hash = 5381; //{1}
for (let i = 0; i < key.length; i++){
hash = hash * 33 + key.charCodeAt(i); //{2}
}
return hash % 1013; //{3}
}
解释一下,5381是一个质数,与33想乘得到一个魔力数。最后得到的相加结果与另一个随机质数1013(这个质数取值一般比我们认为的散列表大小要大)相除得到的余数。
这也许不算是最好的哈希函数,但是被社区推荐。
更多散列函数,可参见:
