树也是一种非线性的数据结构。它对于存储需要快速查找的数据非常有用。有关树的常用术语有:
- 根节点,这个好理解,不多说
- 子树,子树由节点和它的后代构成
- 节点的深度,节点的深度取决于它的祖先节点的数量
- 树的深度,就是所有节点深度的最大值
废话不多说,其实我们对这种结构还是理解挺多的。
树的遍历
先序遍历 – preorder traversal
在先序遍历中,对节点的处理工作是在它的诸儿子节点被处理之前进行的。
后序遍历 – postorder traversal
在后序遍历中,对节点的处理工作是在它的诸儿子节点被计算后进行的。
二叉树 – binary tree
二叉树的节点最多只能有两个子节点: 一个是左侧子节点,另一个是右侧子节点。
二叉树的遍历
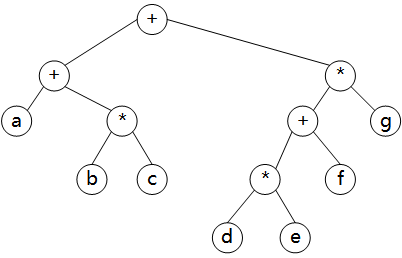
中序遍历 – inorder traversal
先访问左子树,然后根节点,最后右子树。
得到:
(a+b*c) + ((d*e + f)*g)
后序遍历 – postorder traversal
先访问左子树,然后右子树,最后根节点。
得到:
abc+ + de*f + g* +
先序遍历 – preorder traversal
先访问根节点,然后遍历左子树,最后遍历右子树。在遍历左右子树的时候,仍先访问根节点。记为:根左右
得到:
+ +a*bc* + *defg
二叉查找树
二叉查找树是二叉树的一种,它在二叉树的基础上又添加了限制条件: 对于树中的每个节点X,它的左子树中所有关键字的值小于X的关键字的值,而它的右子树中所有关键字的值大于X的关键字的值。
AVL树
AVL(Adelson-Velskii and Landis)树是带有平衡条件的二叉查找树。
这个平衡条件必须容易保持,并且它需保证树的深度是O(log N)。最简单的想法是要求左右子树具有相同的高度。
另一种平衡条件是,要求是要求每个节点都必须要有相同高度的左子树和右子树。
B-树 (B-tree)
这种树也是一种常用的查找树,不是二叉树。
阶为M的B-tree具有下列结构特性:
树的根或者是一片树叶,或者其儿子数在2和M之间
- 除根外,所有非树叶节点的儿子数在
[M/2]和M之间 - 所有的树叶都在相同深度上
红黑树
这是一种特殊的二叉树,这种树可以进行高效的中序遍历。
