• 图的一些概念
  • 相邻顶点
  • 顶点的度
  • 路径
• 图的分类
  • 有向图和无向图
  • 加权图
  • 有环图和无环图
• 图的表示
  • 邻接矩阵
    • 邻接表
• 图的遍历
  • 广度优先搜索
  • 深度优先搜素

图也是一种非线性的数据结构，是网络结构的抽象模型，是一组由边连接的节点。图的表示法:

G = (V,E)，其中V表示一组节点，E表示一组边。

图论的理解有点难度，这里也是介绍一些基本点，仅仅包括图的表示和遍历。因为图论又有好多图，实在是好累。

图的一些概念

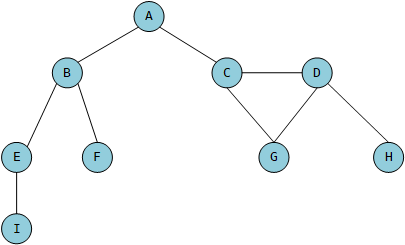
相邻顶点

由一条边连接在一起的顶点叫做相邻顶点。

顶点的度

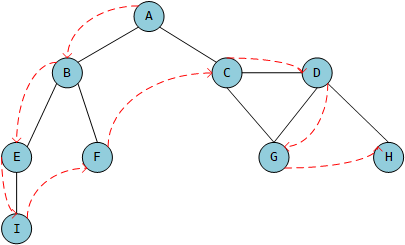
一个顶点的度是其相邻顶点的数量。比如，A的度是3。

路径

路径是顶点v₁,v₂,…,v_k的一个连续序列，其中v_i和v_i+1是相邻的。比如，ABEI就是一条路径。

简单路径要求不包含重复的顶点。

图的分类

有向图和无向图

按照边是否有方向。

加权图

图的边赋予权值。

有环图和无环图

按照图中是否存在环进行的分类。

图的表示

这里仅介绍两种常用的表示方法。

邻接矩阵

如果索引为i的节点和索引为j的节点相邻，则array[i][j] ==== 1；否则，array[i][j] === 0。

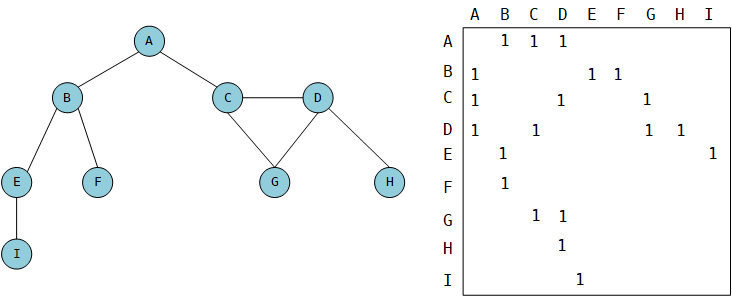
图中为0的部分被省略了，因为画图实在太累。

邻接表

另一种方式就是邻接表。这是一种动态的数据结构，通常情况下，我们会使用链表的结构。

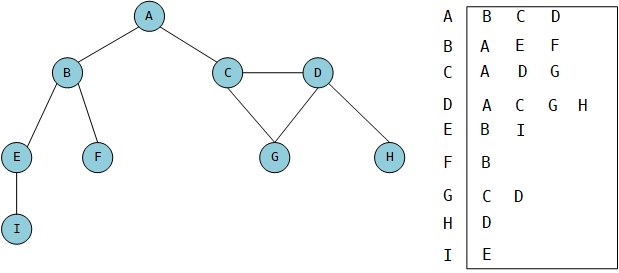
图的遍历

有两种算法可以对图进行遍历: 广度优先搜索(Breadth-First Search, BFS)和深度优先搜索(Depth-First Search, DFS)。图遍历可以用来寻找特定的顶点或寻找两个顶点之间的路径，检查图是否连通，检查图是否含有环等。

图遍历的思想是:

追踪每个第一次访问的节点，并且追踪有哪些节点还没有被完全探索。对于两种遍历方法，都需要指明第一个被访问的顶点。完全探索一个顶点要求我们查看该顶点的每一条边。为了保证算法的效率，务必访问每个顶点至多两次。

广度优先搜索

广度优先搜索的动画演示: Data Structure Visualizations

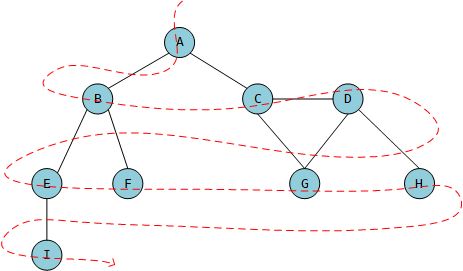
1. 创建一个队列Q
2. 将v标注为被发现，并将v入队列Q
3. 如果Q非空，则:
   1. 将u从Q从出队列；
   2. 标注u为被发现；
   3. 将u所有未被访问过的邻点入队列；
   4. u标注为已被探索。

广度优先搜索的应用: 寻找最短路径

深度优先搜素

深度优先搜索的动画演示: Data Structure Visualizations

深度优先搜索算法将会从第一个指定的顶点开始遍历图，沿着路径直到这条路径最后一个顶点被访问了，接着原路回退并探索下一条路径。

要访问顶点v，步骤如下:

1. 标注v为被发现
2. 对于v的所有未访问的邻点w
1. 访问顶点w(递归)
3. 标注v已被探索

可以看见，深度优先搜索的步骤是递归的。

深度优先搜索的应用：拓扑排序

有关图论还有很多方面，看来我以后得好好啃一下了。拜。